Now available as a fully searchable PDF collection – the Linear Audio USB stick!
See this page for details and ordering info.
Linear Audio provides individualised, custom educational and instructions on request. Programs are developed according to your needs in terms of duration and contents. We can discuss your needs with no obligation. The attached is a sample offering for…
To support then diyaudio Group Buy of Marcel van de Gevel's Tube DAC, here is his article for download.
The valve DAC - Submicron silicon meets submillimetre vacuum…
In Linear Audio Vol 12, Vincent Thiernesse proposed Efficient, unity power-factor, low cost audio power amp supplies. The article discussed the concepts and a general imnplementation. Vincent also wrote about this in the AudioXpress…
For a limited time I offer my Vol 9 article Thermal transient variation of power amp quiescent current - Instrumentation and findings for free download. Enjoy!
Mr. Vogel provided several appendices for his article that did not make it into the printed Volume 13. They are downloadable here; with thanks to author Vogel.
The article in Vol 13 describes the hardware and software setup for an electro-acoustic measurement system based on a soundcard driven by a MathLab / Octave compatible collection of test routines. You can develop your own test routines for your own…
Although Marcel's article in Vol 13 is very complete, some of the more practical desing information like FPGA code and PCB layouts didn't make it into the printed version. Marcel has graciously agreed to make the…
Rudolf has published earlier articles in Linear Audio related to finding the lowest distortion solution for an ultra-linear circuit. However, on closer examination it turned out that his…
Ian Hegglun has published his Cube Law amplifier in Volume 8 and returned in Volume 13 with a CSD (Current Source Driven) output stage. Ian builds on…
Linear Audio Vol 12 contains an article by Hans Polak on the design of a 'non-plus ultra' phono preamp. Hans has kindly agreed to make the PCB layout Gerber files available for…
Bob Coldell´s high quality KT88 tube amp article in Vol 2 generated quite some interest. In fact, I had a friend build one for myself! I designed a small PCB to hold the input and driver stages, to keep te construction clean and repeatable.…
Chris Paul's article looked in much detail into the aspects of Mu followers and related circuitry. Chris developed a spreadsheet and an LTspice file that enabled him (and you) to explore the impact of various variables as explained in the article…
The article by John Escalier in Volume 9 'Semiconductor junction dissipation and temperature - theory and practice' discussed a spreadheet, developed by John, to facilitate calculating the various parameters for thermal management…
Doug Self published a full-fledged preamp design in Volume 5. The design features a sophisticated tone control system. Tone controls have all but disappeared from commercial equipment as implementations were not always high enough quality. However,…
In Vol 6, Hannes Allmaier published his Peter Baxandall - inspired High Octane phono preamp. To facilitate building this preamp, Hannes gives some …
The article from Bruno Putzeys in Vol 5 'The G-word, or, how to get your audio off the ground' is accompanied by a complimentary PCB for the demo project (courtesy Eurocircuits.com). It's a busy PCB and to help with parts placement, a larger version…
In Linear Audio Vol 5, Bruno Putzeys published an excellent article, called “The G Word”, explaining the importance of carefully treating the signal and its reference as a complementary pair of signals and how to prevent uncontrolled connections to (…
Follwing the publication of Volume 10 which contained several articles concerning record replay, John Jones send author Hannes Allmaier and yours truly a long list of effective tip mass data for many…
The following collection of test- and source files was submitted by Scott Wurcer to complement his article on Volume 10 on digital RIAA correction.
For those of you who wish to download the material, there is a pair of .zip files at the end…
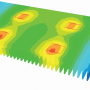Patrick K. (aka EUVL) wrote an interesting article for Vol 3, "…
Linear Technoloy's LTspice simulator is a free, very high performance Spice simulator that is very much appreciated by professional designers and serious hobbyists alike. Gilles Brocart has written an extensive book with reference material,…
In his Volume 7 article Staurt presented a universal gain block, with a particular application to phono preamps. Because it uses JFETs, tubes, MOSFETs and IC regulators, it was baptised 'The Equal Opportunity gain block'.
I designed a PCB layout…
In his Volume 8 article on Cube Law power amplifiers Ian Hegglun mentions that he has a lot of additional information available on the subjet. This additional…
In his article on Audio Equalisation in Volume 7, Malcolm Hawksford provided three Appendices. These contain Matlab scripts that can be used to explore the various circuit concepts described in the…
Stuart Yanigers' Linear Audio Volume 2 article with this title has drawn considerable interest from both audio professionals as well as serious amateurs and hobbyists.
Many readers requested to make it available on line,…